
Shape and Topology optimization of Fluid-Structure Interaction (FSI) problems
This page provides a concise overview of our research on Shape and Topology Optimization applied to FSI problems, which has been the topic of the following publications:
[1] Silva, K.E.S.; Sivapuram, R.; Ranjbarzadeh, S.; Gioria, R. S.; Silva, E. C. N.; Picelli, R. (2022). Topology optimization of stationary fluid–structure interaction problems including large displacements via the TOBS-GT method. Struct Multidisc Optim 65, 337. DOI: https://doi.org/10.1007/s00158-022-03442-3
[2] Siqueira, L. O.; Cortez, R. L.; Sivapuram, R.; Ranjbarzadeh, S.; Gioria, R. dos S.; Silva, E. C. N.; Picelli, R. (2024). Topology optimization for stationary fluid-structure interaction problems with turbulent flow via sequential integer linear programming and smooth explicit boundaries. Adv Eng Softw 190. DOI: https://doi.org/10.1016/j.advengsoft.2024.103599
2.1 – Topology optimization of stationary fluid-structure interaction problems including large displacements [1]
The inclusion of large displacements into the optimization problem allows solutions closer to a realistic design since the structural systems demands nonlinear responses in real working conditions. To illustrate this concept, the classical “the wall” optimization problem including nonlinear structural responses is presented below.
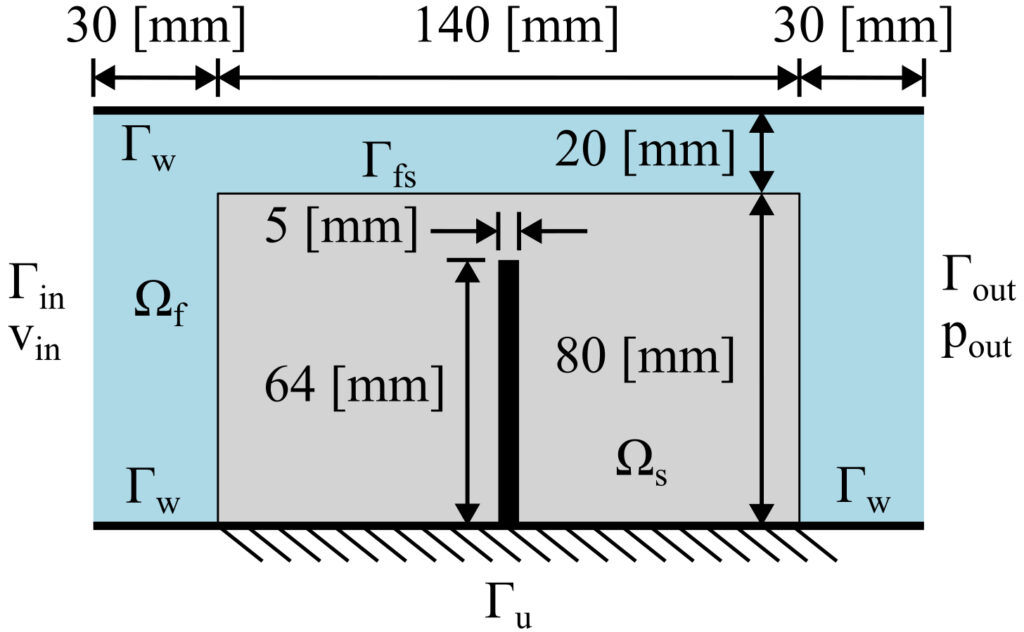
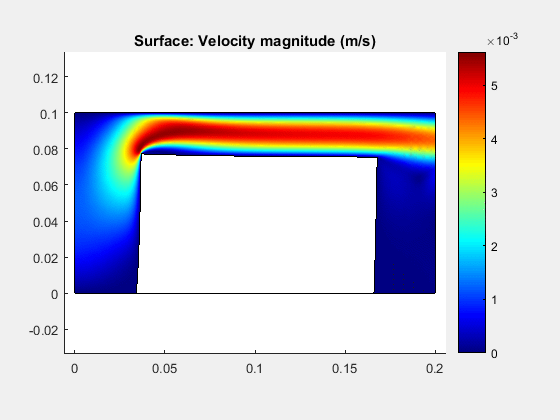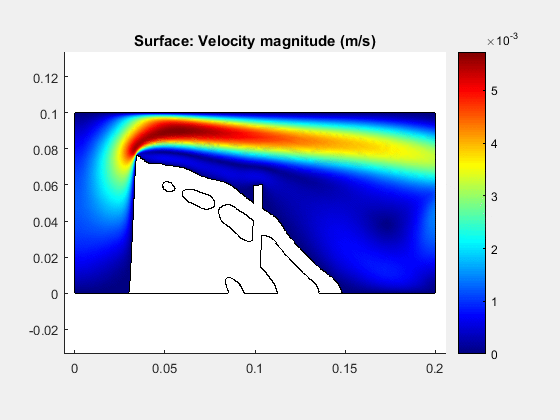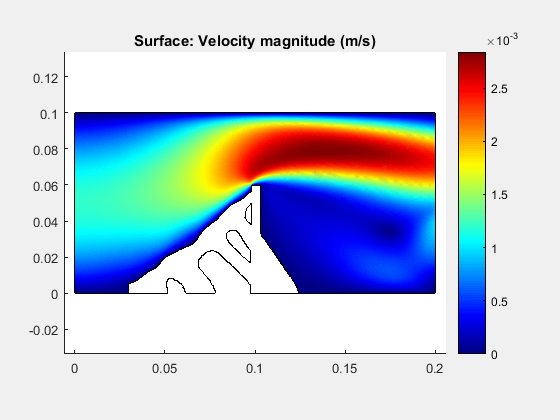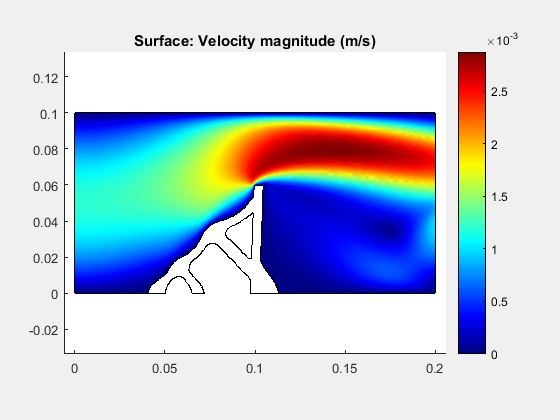
Velocity field and topology evolution for the wall including large displacements
2.2 – Topology optimization of stationary turbulent fluid-structure interaction problems via sequential integer linear programming and smooth explicit boundaries [2]
Most of the works in TO-FSI literature consider laminar flow, which is far from practical applications. In this context, the TOBS-GT method integrated with a smoothing technique based on a phase field function is proposed to solve the FSI turbulent problem. Here, the classical “the wall” example subjected to turbulent flow (Re = 5,000) modeling using the k-ω turbulence model is presented.


Topology evolution for the wall turbulent problem (Re = 5,000)
Contact

Address: Av. Prof. Mello Moraes, 2231 – Polytechnic School of the University of São Paulo, Butantã, São Paulo – SP, 05508-030
Phone: +55 (11) 30915540
Email: rpicelli@usp.br