Mathematical modeling of infectious diseases
We study the dynamics of infectious diseases using mathematical tools and techniques to 
simulate and understand the spread, transmission, and control of various infectious diseases. Through sophisticated and parsimonious modeling approaches, we aim to uncover insights into the complex host-pathogen and environment interactions. Our research explores the efficacy of intervention strategies, the impact of demographic factors, and the dynamics of emerging infectious threats with the ultimate goal of informing public health policies and combating infectious diseases worldwide.
Examples: Corder et al., 2020; Corder et al., 2020; Ferreira et al., 2022.
Genetics-based strategies to control mosquito-borne diseases
Genetics-based vector population modification approaches (also called “replacement”) involve introducing genes that prevent parasite transmission into wild mosquito populations and have several predicted attractive features. In addition to sustainability, they leave no “empty” ecological niche open to invasive species, and thus may be neutral in their environmental impact. Leveraging experimental data, we employ mathematical modeling techniques to gain insights into the efficacy and implications of these genetic interventions.
Examples: Carballar-Lejarazú R et al., 2023; Smidler AL et al., 2023; Auradkar et al., 2024.
Synchronization in heterogeneous networks
Synchronization stands as a pivotal phenomenon in networks, exerting a profound impact across a spectrum of disciplines, including biology, chemistry, and physics, and various man-made systems.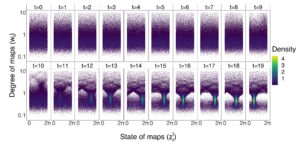 
Notably, recent investigations unveiled the phenomenon of chaotic units achieving sustained and stable cluster synchronization within heterogeneous networks. Because many real-world systems rely on cluster synchronization for their functioning and natural systems often comprise individuals with varying connection counts, understanding the fundamental mechanisms that underlie the spark of synchrony in heterogeneous networks holds promise for elucidating innovative control strategies that amplify coherence among interacting entities.
Examples: Corder et al., 2023; Montalbán and Corder, 2024.